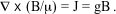
It is well known that electric currents flow more easily along magnetic field lines in a plasma. Taylor recently showed "relaxed" plasma configurations in which the current and magnetic fields are parallel. Theoretically, Taylor said, such a configuration is "self-generating" by a process of magnetic reconnection. Therefore, a plasma ball in this model might quickly adjust itself so that the electric current follows the path of least resistance; that is, where the current density J is parallel to the magnetic field B:
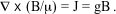
This equation in general has solutions, although the scalar geometric parameter g may have to be a function of position to satisfy boundary conditions. In a sphere, the field and current are helical, like a loop of twisted rope, equivalent to a superposition of poloidal and toroidal components. Helical solutions also exist for a long cylinder of plasma, such as a lightning stroke. A ball arising as an eddy current alongside or around the stroke could then obtain its initial helical structure from the stroke. Because the current and magnetic field are everywhere parallel, the magnetic force JxB is identically zero everywhere, no matter how great the current. Particles, however, could still be trapped by spiralling in the magnetic field, which would reduce somewhat the magnetic permeability, µ.
A ball might form in a pocket of plasma tangent to the stroke with its axis perpendicular to the axis of the stroke. It seems more likely, however, that a ball would form around the stroke with axes coincident. If the stroke itself had a helical field structure, both poloidal and toroidal currents would be efficiently induced in the ball. In this position a ball would also be an effective choke, allowing it to absorb a great deal of energy from the stroke. The induced current opposes any change in the stroke current. When the stroke current begins to decrease, the current in the ball would flow in the same direction as the stroke current.
Spatial deformation of a ball conserves the flux Ø. The magnetic energy Ø2/2L is constant during a deformation, because there is no JxB force to convert the magnetic energy to any other form. Therefore the inductance L is constant. If L changed significantly, a great deal of energy would be released, and the ball would lose plasma and rapidly disintegrate. This agrees with observation; it is consistently reported that balls remain nearly constant in size until disappearance (often by explosion).
The inductive life span of a ball is given by
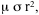
where µ is the magnetic permeability,  is the conductivity, and r is the radius of the ball. It is shown in kinetic theory that;
is the conductivity, and r is the radius of the ball. It is shown in kinetic theory that;
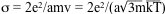 ,
,
where a is the cross-section of an ion; m, v, e the mass, velocity, and charge of an electron; k Boltzmann's constant; and T temperature. According to the CRC tables, the radius of N+ ion is 0.25Å, and 0+ ion is 0.22Å. Assuming an average of 0.24Å and a temperature of at least 15,000K (the same as lightning) the conductivity is found to be approximately 108 mhos/m (which is about the same as that of copper). This gives a lifetime of about one second, which agrees with observation. The quantum mechanical cross-section falls off as the inverse square of the temperature, so the resistance can be made arbitrarily low by choosing a sufficiently high temperature. A ball will be hotter inside, with 15,000K an estimate of the mean. If the temperature falls, the resistance would increase, additional ohmic heating would then drive up the temperature, and vice versa, so that a balance results.
Singer has estimated that the radiative life span of a ball of plasma at atmospheric pressure is about one millisecond. A ball of plasma at atmospheric density, however, would possess about 200 times as much energy, and the opacity would be much greater, resulting in a radiative life span measured in seconds, which agrees with observation. Hence, the life span of a ball of lightning is essentially the inductive or radiative lifetime, both of which are proportional to the square of the radius. The observed luminosity would be produced by an effective surface temperature of about 2,000 K. The opacity given in published tables is consistent with the observed luminosity, which is inversely proportional to the opacity.
If diatomic air is heated to 15,000K (roughly 50 times room temperature) and broken into singly ionized ions and electrons, there are four times as many particles as before. Hence, a pressure of 4x50=200 atmospheres would result. If the energy of the system is a minimum with respect to the particle density, it can be shown that the magnetic permeability is two-thirds of the vacuum value, and the pressure is equal to the vacuum magnetic energy density:
B2/2µo = 200 atmospheres =
2x107N/m2 .
This implies that B is 6 tesla, and from the approximate equation:
B = µI/2r ,
one can deduce that the current I is about one million amperes. As a ball ages, the field weakens and plasma might escape, lightening the ball and forming rays or jets. If a mass m of n moles of plasma leaks and expands adiabatically, most of its internal energy would be converted to kinetic energy:
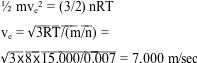 ,
,
where we take the mass per mole of ionized nitrogen to be 0.007 kg, R the ideal gas constant, and T the temperature. Conservation of momentum in the ball's instantaneous restframe requires:
mdv = vedmo
v = veln(mo/m) ,
where v is the velocity of the ball, mo is the initial mass of the ball, and m is the mass remaining after some is ejected at exhaust velocity ve. Since the plasma is very hot and under great pressure, a jet of escaping plasma would act as a sort of rocket propulsion. Balls have also been seen to fall to the ground, roll about, and then rise, suggesting their density decreases.
The energy of ionization in a 0.1 meter ball at atmospheric density is about 4x105 joules; the magnetic energy, 1/2LI2, is about 105 joules; and the power emitted would be about 105 watts, which agrees with high-energy observations.
In a classic observation recorded by Singer, a ball exploded, demolishing a house. The energy of the ball was estimated to be greater than 109 joules. A ball of radius 0.15 meter and current of 50 million amperes would have the density of water and energy of about 109 joules. Singer also notes that balls have been reported to sink in water. Thus our model can account for the most extreme observations. Admittedly these figures seem rather high, but other models are even less plausible, or fail completely.
Balls often make a hissing or crackling sound, as one might expect in view of their electrical nature. The smell of sulphur so often reported is probably just ozone or oxides of nitrogen, copiously produced by the electrical discharge. The large current could easily kill, which has occurred. A ball need not carry any net charge, and the internal potential is only about one volt, which explains why balls show little interest in grounded conductors. Balls should be strongly magnetic, however, which has been verified. As the magnetic field decreases, a ball might become unstable and explode, which also is often observed. Explosion suggests a large internal pressure, consistent with our model.